精彩还要更进一步

教学片段：我们学习了角平分线的性质，下面我们来看一个例题：

已知，如图，AD平分∠BAC，DE⊥AB，DF⊥AC，垂足分别为E、F，求证：AD垂直平分EF

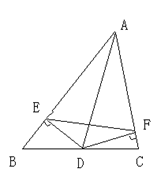
（我的想法是：根据条件AD平分∠BAC，DE⊥AB，DF⊥AC，得出DE＝DF的结论，然后再利用等边三角形的性质或线段垂直平分线的性质，即可证明）

师：观察已知条件，可以得到什么结论？

生1：由已知条件再加上公共边AD，可以证明ΔAED≌ΔAFD，然后再证一次全等就可以了。

下面有学生开始抢着说：“太麻烦了，还有更简单的。”

其实，这道题还是有好些方法解决的，于是，我让学生合作交流，共同来解决这个问题，看看哪一组用的方法更简单。有了竞争，学生讨论起来很激烈，

学生在经过一定时间内经过合作交流，对这个题目给出了4种不同的解法，一种比一种简单，包括了我预设的那种方法。我很高兴，不吝言词的表扬了他们，学生的学习气氛也非常好。然后就是布置作业、检测，而后学生在高兴中下了课。

思考：

在本节课中，当学生提出了解题策略，但彼此间不统一或有争议时，我让学生分组讨论，并鼓励他们，哪一组想到的方法既简便又多？这样就把学生推到了发现者的位置上，使学生带着极大的学习积极性和自信心进行探索与交流，让他们在合作学习中扩大交流面、这样既让他们的意见得到了展示，又使他们在交流中获得思维的碰撞，发现各种证明的方法。但我觉得我对这道例题的处理仅仅停留在了表面的处理上，少了“点睛之笔”。如果我在学生提出的4种解法之后再提出这样的几个问题：为什么想到了这种解法？这几种解法的共性是什么？不同是什么？每一种证明各用了哪些定理？有的证法为什么会简单？从而引导学生把前面所学知识都梳理一遍，这样，学生的知识就系统了，方法请出了，体会到了依托局部构建整体的数学思考方法。做了一个，会了一类，通了一片，这样就能把这一个题目充分利用起来。